Op-Amps en instrumentación y acondicionamiento de señales

Orden del día

• Responder preguntas
• Amplificadores operacionales diferenciales
• Amplificadores operacionales de instrumentación
• Estudiemos como acondicionar señales con OpAmps

Amplificadores Operacionales

Ecuación:

$$V_{out} =K (V^+-V^-)$$

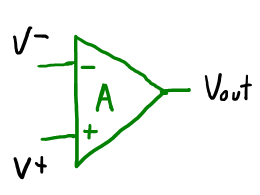
Amplificador en realimentación negativa

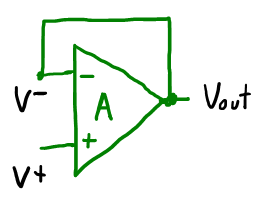
Demostrar a partir de la ecuación $V_{out} =K (V^+-V^-)$ que $V^+=V^-$. (Usar diagrama de bloques de un sistema en lazo cerrado?)

Solución

Teniendo que $ V_{out} = K \left(V^{+} - V^{-}\right)$ por definición y $V_{out} = V^{-}$ por la realimentación. Por igualación tendremos:

vout,vp,vm,K = symbols("V_{out},V^+,V^-,K")
eq1 = Eq(vout,K*(vp-vm))
eq2 = eq1.subs({vout:vm})
display(eq2)
print("despejando")
eq3 = Eq(vm,solve(eq2,vm)[0])
display(eq3)
print("aplicando el límite")
display(Eq(vm,Limit(eq3.rhs,K,oo)))
print("luego")
display(Eq(vm,limit(eq3.rhs,K,oo)))

$\displaystyle V^{-} = K \left(V^{+} - V^{-}\right)$

despejando

$\displaystyle V^{-} = \frac{K V^{+}}{K + 1}$

aplicando el límite

$\displaystyle V^{-} = \lim_{K \to \infty}\left(\frac{K V^{+}}{K + 1}\right)$

luego

$\displaystyle V^{-} = V^{+}$

Opamps diferenciales

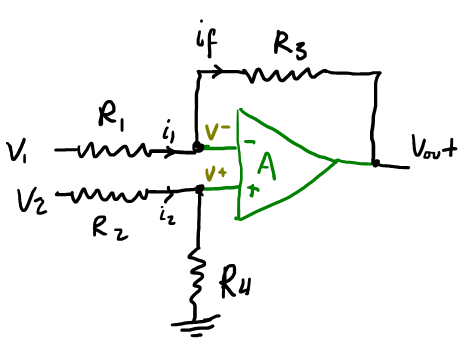
Ecuación: $$V_{out} = -\left(\frac{R_3}{R_1}\right)\,V_1 + \left(\frac{R_3+R1}{R_1}\right)\left(\frac{R_4}{R_2+R_4}\right)\,V_2$$

Opamps de instrumentación

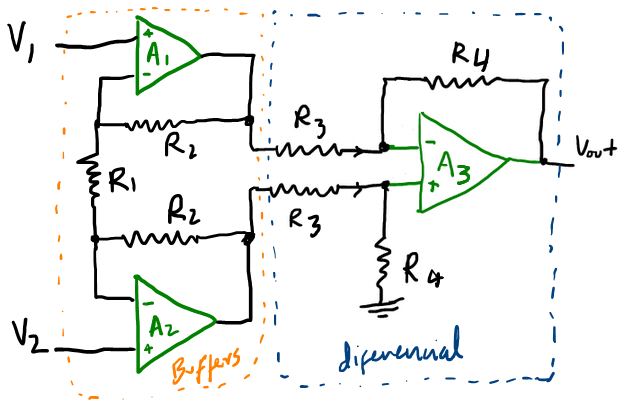
Encontrar la ecuación para la variable de salida $V_{out}$ en función de $V_1$ y $V_2$.

Solución

En este sistema tenemos un amplificador diferencial que responde a su ecuación:

v3o,v1o,v2o,v3p,v1,v2 = symbols("V_{out},V_1^{out},V_2^{out},v_3^+,V_1,V_2 ")
R1,R2,R3,R4,i1 = symbols("R_1,R_2,R_3,R_4,i_1")

ec3 = Eq(v3o,-R3/R1*v1o + ((R3+R1)/R1)*(R4/(R2+R4))*v2o)
display(ec3)
ec3 = factor(ec3.subs({R2:R1,R3:R4}))
ec3 = ec3.subs({R1:R3})
print("igualando la resistencia en concordancia con la imagen, tenemos que:")
display(ec3)

$\displaystyle V_{out} = - \frac{R_{3} V_1^{out}}{R_{1}} + \frac{R_{4} V_2^{out} \left(R_{1} + R_{3}\right)}{R_{1} \left(R_{2} + R_{4}\right)}$

igualando la resistencia en concordancia con la imagen, tenemos que:

$\displaystyle V_{out} = - \frac{R_{4} \left(V_1^{out} - V_2^{out}\right)}{R_{3}}$

Para los buffers calcularemos lo siguiente:

ec1a = Eq(i1,(v1o-v1)/R2)
ec1b = Eq(i1,(v2-v2o)/R2)
ec1c = Eq(i1,(v1-v2)/R1)

display(ec1a)
display(ec1b)
display(ec1c)

print("Resolviendo el sistema de ecuaciones")
sols = solve([ec1a,ec1b,ec1c],{v1o,v2o,i1})
display(sols)

$\displaystyle i_{1} = \frac{- V_{1} + V_1^{out}}{R_{2}}$

$\displaystyle i_{1} = \frac{V_{2} - V_2^{out}}{R_{2}}$

$\displaystyle i_{1} = \frac{V_{1} - V_{2}}{R_{1}}$

Resolviendo el sistema de ecuaciones

$\displaystyle \left\{ V_1^{out} : \frac{R_{1} V_{1} + R_{2} V_{1} - R_{2} V_{2}}{R_{1}}, \ V_2^{out} : \frac{R_{1} V_{2} - R_{2} V_{1} + R_{2} V_{2}}{R_{1}}, \ i_{1} : \frac{V_{1} - V_{2}}{R_{1}}\right\}$

Remplazando la ecuación de los buffers en el amplificador diferencia tendremos:

display(factor(expand(ec3.subs(sols))))

$\displaystyle V_{out} = - \frac{R_{4} \left(R_{1} + 2 R_{2}\right) \left(V_{1} - V_{2}\right)}{R_{1} R_{3}}$

Rescrito de otra forma:

$$V_{out} = (V_2-V_1)\left(1+\frac{2R_2}{R_1}\right)\left(\frac{R_4}{R_3}\right)$$

Acondicionamiento de señales

Ejercicio de aplicación del sensor PT500

Dado un sensor PT500 con la siguiente expresión matemática en el rango de 0°C a 850°C

$$R(T) =R_0\,(1 + A \cdot T + B \cdot T^2)$$

donde $R_0 = 500$, $A=3.9083e-3$ y $B=-5.775e-7$

Seleccionar el circuito potenciométrico (divisor de voltaje o puente de deflexión) y las resistencias de este circuito y de amplificador operacional de instrumentación para un rango de temperatura de un proceso biotecnológico (0°C a 50°C) y que se acondicione la señal para ser recibida en un microcontrolador de 3.3V de 12 bits.

Realizar un análisis de las características estáticas del sistema de medida.

# En python
R0 = 500; A = 3.9083e-3; B = -5.775e-7
R = lambda T : R0 * (1 + A * T + B * T**2)

Respuesta del sensor PT500 en el rango de 0°C a 850°C

tp = np.arange(0,850,1)
rp = R(tp)

plt.plot(tp,rp)
plt.grid()
plt.xlabel("Temperatura [°C]")
plt.ylabel("Resistencia [Ω]");

Respuesta del sensor PT500 en el rango de 0°C a 50°C

tp = np.arange(0,50,0.1)
rp = R(tp)

plt.plot(tp,rp)
plt.grid()
plt.xlabel("Temperatura [°C]")
plt.ylabel("Resistencia [Ω]");

Tener en cuenta el ruido blanco que aparece en las señales electrónicas!

ruido blanco en python