Control en espacio de estados¶

Orden del día¶

Responder preguntas
Diseñar un controlador
Agregar el control integral

Ejemplo de control en un tanque¶

Tomando la ecuación diferencial para un tanque con una entrada de caudal y un salida de caudal atmosferica, siendo:

$$A\,\frac{d}{dt}h(t) = q_{in}(t)- \frac{h(t)}{R}$$

donde $A$ es el area del tanque (suposición de que el area es constante), $R$ es la resistencia hidráulica, una constante que aparece despues de linealizar la ecuación. $h(t)$ es la altura del tanque y $q_{in}(t)$ es el caudal de entrada.

Construyamos un controlador para este sistema.

Solución 1/6¶

Inicialmente llevemos la ecuación diferencial $A\,dh(t)/dt = q_{in}(t)- {h(t)}/{R}$ a la representación en espacio de estados:

$$\begin{align} \dot{x} &=& \begin{bmatrix}-\frac{1}{AR}\end{bmatrix} &\,x + \begin{bmatrix}\frac{1}{A}\end{bmatrix}\,u \\ y&=&\begin{bmatrix}1\end{bmatrix}&\,x \\ \end{align} $$

De aquí podremos llevar el sistema a un lazo cerrado:

$$\dot{x}=\left(A-BKC\right)\,x + B\,r$$

Solución 2/6¶

El diagrama de bloques en lazo cerrado es:

Solucion 3/6¶

Teniendo un controlador $K=[K_p]$, la matrix dinámica del sistema en lazo cerrado será:

$$A=\begin{bmatrix}-\frac{Kp}{A}-\frac{1}{AR}\end{bmatrix}$$

De aquí podemos ver que el sistema es estable para valores positivos de $K_p$, suponiendo todos los valores de los parámetros en $1$, la respuesta del sistema es:

plt.plot(t,y,[t[0],t[-1]],[1,1]);
plt.legend(["salida","referencia"])
plt.xlabel("tiempo");
plt.ylabel("amplitud");

No description has been provided for this image

Solución 4/6¶

Cómo pudimos observar la salida no llega a la referencia. Si pensamos en el control $PID$, en este momento tenemos un controlador tipo $P$. Para agregar un controlador $PI$ deberemos agregar un tercer lazo cerrado (el segundo lazo de control) al sistema:

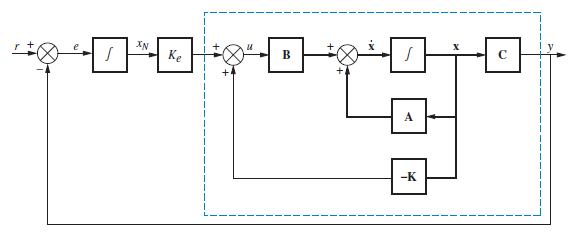
La representación en espacio de estados será:

$$\begin{align} \begin{bmatrix} \dot{x}\\ \dot{x_N} \end{bmatrix}&= \begin{bmatrix} (A-BK) & B\,K_e \\ -C & 0 \end{bmatrix} \,\begin{bmatrix} x\\ x_N \end{bmatrix}+ \begin{bmatrix} 0\\ 1 \end{bmatrix} \,r \\ y&= \begin{bmatrix} C & 0 \end{bmatrix} \,\begin{bmatrix} x\\ x_N \end{bmatrix} \end{align}$$

Solución 5/6¶

Remplazando los valores en la ecuación, tendremos (con $K_e=1$):

Ke = 1
mKe = np.array([[Ke]])
nA = np.stack((np.stack((mA,mB*mKe),axis=2),np.stack((-mC,np.array([[0]])),axis=2)))
nB = np.array([[0],[1]])
nC = np.stack((mC,np.array([[0]])),axis=2)

nA = nA.reshape((2,2))
nC = nC.reshape((1,2))

sys = ct.ss(nA,nB,nC,mD)
display(sys)

$$ \left(\begin{array}{rllrll|rll} -2\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}\\ -1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}\\ \hline 1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}\\ \end{array}\right) $$

Esta notación incluye las matrices $A$, $B$, $C$ y $D$.

Solución 6/6¶

Haciendo la simulación del sistema en lazo cerrado con lazo de integración, la respuesta temporal será:

plt.plot(t,y,[t[0],t[-1]],[1,1]);
plt.legend(["salida","referencia"])
plt.xlabel("tiempo");
plt.ylabel("amplitud");

Los valores propios de la matriz $A$ son: $-1$ con multiplicidad $2$

Posicionamiento de polos¶

Tomando de manera teórica los valores del sistema en lazo cerrado tendremos la matrix dinámica del sistema

Ke,l = symbols("K_e,\\lambda")
MKE = Matrix([[Ke]])

NA = Matrix([[MA-MB*MK,MB*MKE],[-MC,Matrix([[0]])]])
display(NA)

$\displaystyle \left[\begin{matrix}- \frac{K_{p}}{A} - \frac{1}{A R} & \frac{K_{e}}{A}\\-1 & 0\end{matrix}\right]$

Podemos calcular la ecuación carasterística:

EC = Poly((l*eye(2) - NA).det(),l)
display(EC)

$\displaystyle \operatorname{Poly}{\left( \lambda^{2} + \frac{K_{p} R + 1}{A R} \lambda + \frac{K_{e}}{A}, \lambda, domain=\mathbb{Z}\left(A, K_{e}, K_{p}, R\right) \right)}$

Podemos igualar con el polinomio generado por dos polos:

p1,p2 = symbols("p_1,p_2")
poles2 = Poly((l-p1)*(l-p2),l)
display(poles2)

$\displaystyle \operatorname{Poly}{\left( \lambda^{2} + \left(- p_{1} - p_{2}\right) \lambda + p_{1} p_{2}, \lambda, domain=\mathbb{Z}\left[p_{1}, p_{2}\right] \right)}$

Posicionamiento de polos (continuación)¶

Igualando los coeficientes:

C1 = poles2.coeffs()
C2 = EC.coeffs()

eq1 = Eq(C1[1],C2[1])
eq2 = Eq(C1[2],C2[2])

display(eq1,eq2)

$\displaystyle - p_{1} - p_{2} = \frac{K_{p} R + 1}{A R}$

$\displaystyle p_{1} p_{2} = \frac{K_{e}}{A}$

Resolviendo

sols = solve({eq1,eq2},{Kp,Ke})
display(sols)

$\displaystyle \left\{ K_{e} : A p_{1} p_{2}, \ K_{p} : \frac{- A R p_{1} - A R p_{2} - 1}{R}\right\}$

Posicionamiento de polos (continuación)¶

Si deseamos ubicar los polos del sistema en $-5$ y $-30$, tendremos:

K1 = Eq(Kp,sols[Kp].subs({p1:-5,p2:-30}))
K2 = Eq(Ke,sols[Ke].subs({p1:-5,p2:-30}))
display(K1,K2)

$\displaystyle K_{p} = \frac{35 A R - 1}{R}$

$\displaystyle K_{e} = 150 A$

suponiendo valores unitarios, tendremos:

display(K1.subs({A:1,R:1}))
display(K2.subs({A:1,R:1}))

$\displaystyle K_{p} = 34$

$\displaystyle K_{e} = 150$

Posicionamiento de polos (continuación)¶

La respuesta temporal para el sistema en lazo cerrado será:

nAe = np.array(NA.subs({Kp:34,Ke:150,A:1,R:1})).astype(np.float64)

sys = ct.ss(nAe,nB,nC,mD)
t,y = ct.step_response(sys)
display(sys)
plt.plot(t,y,[t[0],t[-1]],[1,1]);
plt.legend(["salida","referencia"])
plt.xlabel("tiempo");
plt.ylabel("amplitud");

$$ \left(\begin{array}{rllrll|rll} -35\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&150\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}\\ -1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}\\ \hline 1\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}&0\phantom{.}&\hspace{-1em}&\hspace{-1em}\phantom{\cdot}\\ \end{array}\right) $$

Ejercicios¶

Considerando la siguiente representación en espacio de estados:

$$\begin{align} \dot{x}&= \begin{bmatrix} 0 & 1 \\ -3 & -5 \end{bmatrix} \,x+ \begin{bmatrix} 0\\ 1 \end{bmatrix} \,u \\ y&= \begin{bmatrix} 1 & 0 \end{bmatrix} \,x \end{align}$$

Diseñar un controlador sin control integral que genere un sobre pico del $10\%$ y un tiempo de establecimiento de $0.5$ segundos. Evaluar el error en estado estacionario para un escalón unitario.
Repita el diseño del controlador incluyendo el control integral. Evaluar el error en estado estacionario para un escalón unitario.

Sobre el sobre-pico¶

El sobre pico se puede definir en función de coeficiente de amortigüamiento $\xi$, de la siguiente forma:

$$S_p = e^{-\frac{\pi \xi}{\sqrt{1-\xi^2}}}$$

donde $S_p$ es el sobrepico expresado en decimal luego,

sp,xi = symbols("S_p,\\xi")
display(Eq(xi,solve(Eq(sp,exp(-pi*xi/sqrt(1-xi**2))),xi)[0]))

$\displaystyle \xi = \frac{\log{\left(\frac{1}{S_{p}} \right)}}{\sqrt{\log{\left(\frac{1}{S_{p}} \right)}^{2} + \pi^{2}}}$

Relación entre el amortiguamiento y los polos¶

Existe una relación entre el amortiguamiento y el valor de los polos, se puede ver en la siguiente gráfica

Referencias¶

Nise, Norman S. Sección 12. Control systems engineering (7th Ed).