Op-Amps diferenciales
Para entender los amplificadores operacionales diferenciales debemos primero entender el funcionamiento de un amplificador operacional con realimentación negativa.
Opamp
Un amplificador operacional es una abstracción funcional de circuitos analógicos que se representan de la siguiente forma:
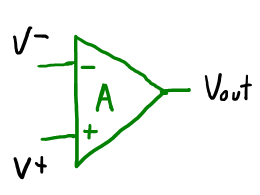
Cuenta con los entradas y una salida normalmente $V_{out} =K (V^+-V^-)$, para el funcionamiento del amplificador se tienen dos terminales de alimentación:
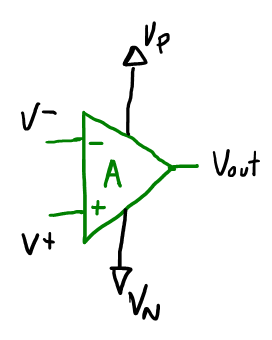
Opamp con realimentación negativa
Todos los tipos de funcionamiento del amplificador operacional no serán explicados aquí. Nos concentraremos en el función del amplificador con realimentación negativa.
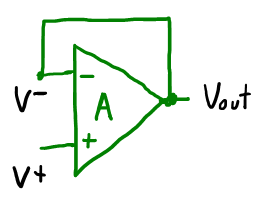
Cuando se tiene realimentación negativa ocurre lo siguiente:
- No fluye corriente hacia el amplificador por los terminales $V^+$ y $V^-$.
- El voltaje de los terminales de entrada es el mismo $V^+ = V^-$.
Ejemplo
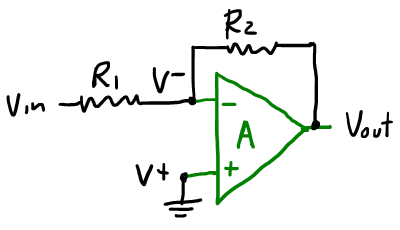
Encontrar la función $V_{out}$ en terminos de las resistencias y el voltaje de entrada $V_{in}$
Dado que no hay corriente que fluya hacia el amplificador en el nodo $V^-$ entonces la corriente que fluye de $V_{in}$ a $V^-$ es la misma que fluye de $V^-$ a $V_{out}$, luego:
\[\frac{V_{in}-V^-}{R_1} = I = \frac{V^--V_{out}}{R_2}\]Teniendo que $V^+ = V^-$ y $V^+=0$, luego $V^-=0$, por lo que la ecuación anterior se reduce:
\[\frac{V_{in}}{R_1} = \frac{-V_{out}}{R_2}\]Despejando, obtenemos:
\[V_{out} = - \frac{R_2}{R_1}\,V_{in}\]Opamps diferenciales
Un amplificador diferencial básicamente es un amplificador en realimentación negativa con dos voltajes de entrada $V_1$ y $V_2$, como se muestra a continuación:
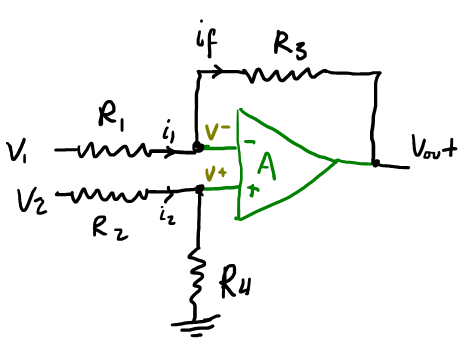
Encontrar la relación del voltaje de salida $V_{out}$ y los voltajes de entrada $V_1$ y $V_2$.
Recordando que no hay corrientes que ingresen al amplificador por los terminales de entrada tendremos que:
\[i_1 = i_f \qquad\text{y}\qquad i_2 = i_4\]remplazando las corrientes con la ley de Ohm, tenemos:
\[\frac{V_1-V^-}{R_1} = \frac{V^--V_{out}}{R_3} \label{d1}\] \[\frac{V_2-V^+}{R_2} = \frac{V^+}{R_4} \label{d2}\]Despejando $V^+$ de \eqref{d2},
\[V^- = V^+ = \frac{R_4}{R_2+R_4} \,V_2 \label{d3}\]Despejando $V_{out}$ de \eqref{d1},
\[V_{out} = -\frac{R_3}{R_1}\,V_1 + \frac{R_3+R1}{R_1}\,V^- \label{d4}\]Remplazamos \eqref{d3} en \eqref{d4}:
\[V_{out} = -\left(\frac{R_3}{R_1}\right)\,V_1 + \left(\frac{R_3+R1}{R_1}\right)\left(\frac{R_4}{R_2+R_4}\right)\,V_2 \label{d5}\]Asumiendo $R_1=R_2$ y $R_3=R_4$, tendremos:
\[V_{out} = \left(\frac{R_3}{R_1}\right)\left(V_2-V_1\right) \label{d6}\]Opamps de instrumentación
El amplificador operacional de instrumentación agrega otros dos amplificadores a modo de aislar las entradas con el siguiente circuito.
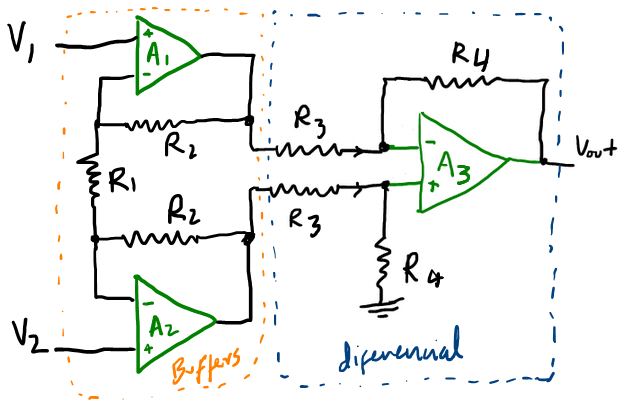
Encontrar la relación del voltaje de salida, con los voltajes de entrada.
Acondicionamiento de señales
El acondicionamiento de señales nos permite obtener el mayor beneficio (información o granularidad de los datos) con los recursos que cuenta un sistema de medida.
Ejemplo introductorio
Supongamos que la escala de salida de un sistema de medida va de $0$ a $0.5\,V$, y tenemos un Arduino que nos permite tener una lectura analógica de voltaje de $0$ a $5\,V$. En este caso, si no acondicionamos la medida, estaremos utilizando solo el $10\%$ del rango de entrada en el Arduino. Para el caso de un Arduino UNO/MEGA, el conversor analógico-digital cuenta con $10$ bits. Lo que significa que tendremos $2^{10} = 1024$ valores diferente en la lectura. Usando solo el $10\%$ del rango supondrá medir solamente $10\% \times 1024 \approx ~ 102$ valores. Es decir, una resolución de $500\,mV/102 \approx 5\,mV$.

Si hacemos un acondicionamiento de la señal, que en este caso puede ser multiplicar $\times 10$ la salida del sistema de medida antes de llevarla al Arduino, esto generará una señal a la salida del sistema de acondicionamiento de $0$ a $5\,V$. Esto nos permitirá usar el $100\%$ de la escala del Arduino, lo que mejorara la resolución del sistema global. Tendremos una resolución del $500\,mV/1024 \approx 0.5\,mV$

Acondicionamiento
En el ejemplo anterior modificamos la curva de sensibilidad del sensor pasando de $0.5 [V/fs]$ ($fs$ siendo la full scale la escala completa de la variable de entrada) a $5 [V/fs]$. De la misma forma podemos modificar los atributos de la ecuación de la linea recta para mejorar el registro de los valores del sensor.
\[y = a \,x + b\]