Controlabilidad

Los métodos de espacio de estados pueden ser usados en una más amplia variedad de sistemas que el metodo de transformada, tanto para sistemas lineales como no lineales. Aunque aquí solo abordaremos sistemas lineales o linealizados.

Diseño de un controlador

Para diseñar un controlador en espacio de estados, podemos usar un método conocido como posicionamiento de polos, este nos permitira modificar la posición de los polos del sistema por lo tanto podremos hacer que el sistema tenga las respuesta transitoria y estacionaria que queramos.

Para hacer el posicionamiento de polos usaremos la ecuación caracteristica \eqref{caracteristica} del sistema la cual tiene $n$ coeficientes para un sistema de orden $n$, la cuales pueden ser modificada a nuestra conveniencia. Todo esto es posible si el sistema cumple con ciertas condiciones.

Consideremos la representación del sistema en espacio de estados sin matrix directa:

\[\begin{align} \dot{x}&=A\,x+B\,u \label{state_equation} \\ y&=C\,x \label{output_equation} \end{align}\]

Estas ecuaciones pueden ser visualizadas en el siguiente diagrama de bloques:

Si realizamos un lazo cerrado del sistema usando la realimentación de estados tendremos la imagen (b), y las ecuaciones serán:

\[\begin{align} \dot{x}&=A\,x+B\,u \\& =A\,x+B(-K\,x+r) \\& =(A-BK)\,x+B\,r \\ y&=C\,x \end{align}\]

Con esta nueva representación (teniendo $C=I$, lo que es igual a la realimentación de estado) podemos encontrar la ecuación caracteristica del sistema en lazo cerrado:

\[\text{det}(sI-(A-BK)) = 0\label{caracteristica}\]

dicha ecuación dependerá de los valores de la matriz $K$, construyendo otra ecuación caracteristica con los polos posicionados por nuestra cuenta.

\[\sum_{i=1}^n (s-p_i) = 0\]

podremos hacer una igualación término a término y encontrar los valores de $k_i$ que cumplan las todas las igualdades. Igualar estos términos y obtener los valores de controlador $K$ es posible solo si el sistema es completamente controlable. Para verificar si un sistema es completamente controlable analicemos la controlabilidad.

Controlabilidad

Un sistema es completamente controlable si somos capacez de llevar al sistema a un estado final $x^\star$, a partir de un estado inicial $x_0$ y conociendo las acciones del sistema en un número $n$ de pasos. Esto es posible si el actuador del sistema es capaz de modificar directa o indirectamente todos los estados del sistema.

En un ejemplo modesto, teniendo un sistema en tiempo discreto:

\[x_{k+1}= A\, x_k + B\, u_k\qquad x_0 = 0\]

llevemos al sistema en un número $n$ de pasos a $x_f$:

\[\array{ x_1 &=& Ax_0 + Bu_0 &=& Bu_0\\ x_2 &=& Ax_1 + Bu_1 &=& ABu_0 + Bu_1\\ x_3 &=& Ax_2 + Bu_2 &=& A^2Bu_0+ ABu_1 + Bu_2\\ &&\vdots\\ x_n &=& Ax_{n-1} + Bu_{n-1} &=& A^{n-1}Bu_0 + \cdots + Bu_{n-1} }\]

el anterior sistema de ecuaciónes puede ser escrito como:

\[x^\star = \left[\array{B&AB&\cdots&A^{n-1}B}\right] \left[\array{u_{n-1} \\ \vdots \\ u_1 \\ u_0}\right] = \Gamma \left[\array{u_{n-1} \\ \vdots \\ u_1 \\ u_0}\right]\]

$\Gamma$ se conoce como la matriz de controlabilidad y determina si el sistema es completamente controlable. Es posible llegar a un estado $x^\star$ si y solo si:

\[\text{rank}\left(\Gamma\right) = n\]

Si se obtiene un rango para gamma inferior a $n$ tenemos un sistema que no es completamente controlable y en ese caso no podremos hacer el procedimiento de asignación de polos.

Control Integral

Con los métodos anteriores tendremos un controlador que tendrán en cuenta el control proporcional y en algunos casos tambien el control derivativo, en caso de que tengamos como variable de estado la derivada de la variable que queremos controlar. Para agregar el componente integral del control clásico al control en espacio de estados tendremos, que agregar los siguientes bloques al sistema:

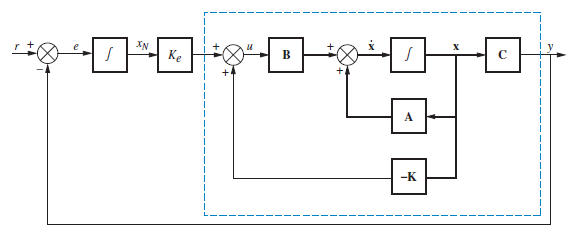
se desarrolla una representación en espacio de estados con la nueva variable y se define el valor de $K_e$.

\[\begin{align} \begin{bmatrix} \dot{x}\\ \dot{x_N} \end{bmatrix}&= \begin{bmatrix} (A-BK) & B\,K_e \\ -C & 0 \end{bmatrix} \,\begin{bmatrix} x\\ x_N \end{bmatrix}+ \begin{bmatrix} 0\\ 1 \end{bmatrix} \,r \\ y&= \begin{bmatrix} C & 0 \end{bmatrix} \,\begin{bmatrix} x\\ x_N \end{bmatrix} \end{align}\]

Aquí nuevamente podremos asignar los polos del controlador.

Realimentación de estado

La realimentación de estado es tomar el estado actual del sistema y entregarlo al controlador en lazo cerrado del sistema, la realimentación no se hace con la medida $y$ sino con son el estado $x$ esto se logra con una matrix de salida $C=I$ o con un observador. Los observadores son explicados aquí.

\[y = C x = I x = x\]

Referencia

• Sección 12.3 de Norman S. Nise (2014). Control Systems Engineering (7th Ed).